Math Assistant – An Agentic Framework for Outlining Proofs

#   Author:
#                   Matt Tucker
#
#   Date:
#                   1Sep2024 - 19Sep2024
#
#   Description:
#                   Math Assistant is an agentic framework for outlining proofs and solutions.
#                   To use the Math Assistant set "math_problem =" to your question.
#                   The agents will work together to outline 3 possible proofs.
#                   Each proof will be saved along with a score and reasoning behind the proof.
#

import os
from langchain_openai.chat_models import ChatOpenAI
from langchain.schema import SystemMessage, HumanMessage, AIMessage
import openai

# Set OpenAI API key
openai.api_key = os.environ['OPENAI_API_KEY']

# Initialize OpenAI Chat LLM
llm = ChatOpenAI(model_name='gpt-4o-2024-05-13', temperature=0.7) # Changed model to 'gpt-3.5-turbo'

# Define mathematical branches
branches = [
    'Algebra',
    'Analysis',
    'Geometry',
    'Number Theory',
    'Combinatorics',
    'Probability and Statistics',
    'Logic and Foundations',
    'Applied Mathematics',
    'Discrete Mathematics',
    'Mathematical Physics',
    'Computational Mathematics',
    'Mathematical Biology'
]

# Function for each math agent
def agent_response(agent_name, conversation_history, math_problem):
    # Build the messages
    messages = []

    # System prompt
    system_prompt = f"You are a professor of mathematics specializing in {agent_name}."
    messages.append(SystemMessage(content=system_prompt))

    # Add conversation history
    if conversation_history:
        for message in conversation_history:
            if message['agent'] == agent_name:
                messages.append(AIMessage(content=message['message']))
            else:
                messages.append(HumanMessage(content=f"{message['agent']}: {message['message']}"))

    # Add the current task
    user_prompt = f"""
The problem to solve is:
{math_problem}

As an expert in {agent_name}, contribute to the discussion to develop an outline for a mathematical proof or solution to the provided problem.

Remember to follow these guidelines:
- Provide insights from your field that can help in constructing the proof.
- Suggest possible approaches or techniques from your field.
- Ask for clarification if needed.
- Use analogies to help conceptualize the problem and the proof/solution.
- Use analogies to help conceptualize the techniques used in the proof/solution.
- Use analogies to help conceptualize past approaches to the problem and why they did or did not work.
- Ask questions about analogies used by the other mathematicians.
- Ask questions about the techniques used by the other mathematicians.
- Work towards agreeing on one valid and complete, step-by-step, cohesive outline of a proof/solution.
- Each step in the outline should be a single, cohesive step.
- Each step in the outline should build on a previous step or be the building block for a future step.
- All steps should ultimately be related to each other and should be related to the overall goal of the proof/solution.
- A good technique for the outline to use would be to start from the intial setup and the goal of the proof/solution and search for a path that will lead to the proof/solution.
- The outline should be of a single approach to the proof/solution, not multiple approaches.
- The final outline of a solution/proof should allow for little to no ambiguity.
- The final proof/solution should require little to no critical thinking on the part of the reader.
- The final proof/solution should be concise and clear.
- A mathematician should be able to solve the problem by following the outline with minimal help/aid from outside resources.

Your response:
"""
    messages.append(HumanMessage(content=user_prompt))

    # Get response from LLM using 'invoke'
    response = llm.invoke(messages).content  # Updated method call
    return response.strip()

# Moderator agent
def moderator_response(conversation_history, math_problem):
    # Build the messages
    messages = []

    # System prompt
    system_prompt = "You are the moderator of this discussion among mathematics professors."
    messages.append(SystemMessage(content=system_prompt))

    # Add conversation history
    if conversation_history:
        for message in conversation_history:
            if message['agent'] == 'Moderator':
                messages.append(AIMessage(content=message['message']))
            else:
                messages.append(HumanMessage(content=f"{message['agent']}: {message['message']}"))

    # Add the current task
    user_prompt = f"""
The problem to solve is:
{math_problem}

As the moderator, assess whether a valid and complete outline of a proof/solution has been generated.

If the agents and you have agreed on a valid and complete outline, respond with 'terminate'.

Otherwise, guide the discussion to help the agents reach agreement.

An outline for a proof/solution should be a step-by-step guide for a single cohesive proof/solution.

While it is good that the agents are working towards a single cohesive proof/solution, it is more important that the proof/solution is valid and complete.

Also, the outline should be of a single approach to the proof/solution, not multiple approaches.

The final outline of a solution/proof should allow for little to no ambiguity.

The final proof/solution should require little to no critical thinking on the part of the reader.

The final proof/solution should be concise and clear.

Your response:
"""
    messages.append(HumanMessage(content=user_prompt))

    # Get response from LLM using 'invoke'
    response = llm.invoke(messages).content  # Updated method call
    return response.strip()

# Function to get final outputs from the moderator
def moderator_final_output(conversation_history, math_problem):
    # Build the messages
    messages = []

    # System prompt
    system_prompt = "You are the moderator of this discussion among mathematics professors. You're job is to moderate the discussion and ensure that the agents are working towards a valid and complete outline of a proof/solution. You're job is not to solve the problem, but to ensure that the agents are working towards a single valid and complete outline of a proof/solution. The agents should be working towards ONE cohesive proof/solution with their outline."
    messages.append(SystemMessage(content=system_prompt))

    # Add conversation history
    if conversation_history:
        for message in conversation_history:
            if message['agent'] == 'Moderator':
                messages.append(AIMessage(content=message['message']))
            else:
                messages.append(HumanMessage(content=f"{message['agent']}: {message['message']}"))

    # Add the current task
    user_prompt = f"""
Since the agents have agreed on a valid and complete outline of a proof/solution, please provide the following:

- A score for how likely the proof/solution is to work.
- The outline of the proof/solution using LaTeX formatting.
- The reasoning behind the outline.

Your response should be formatted as follows:

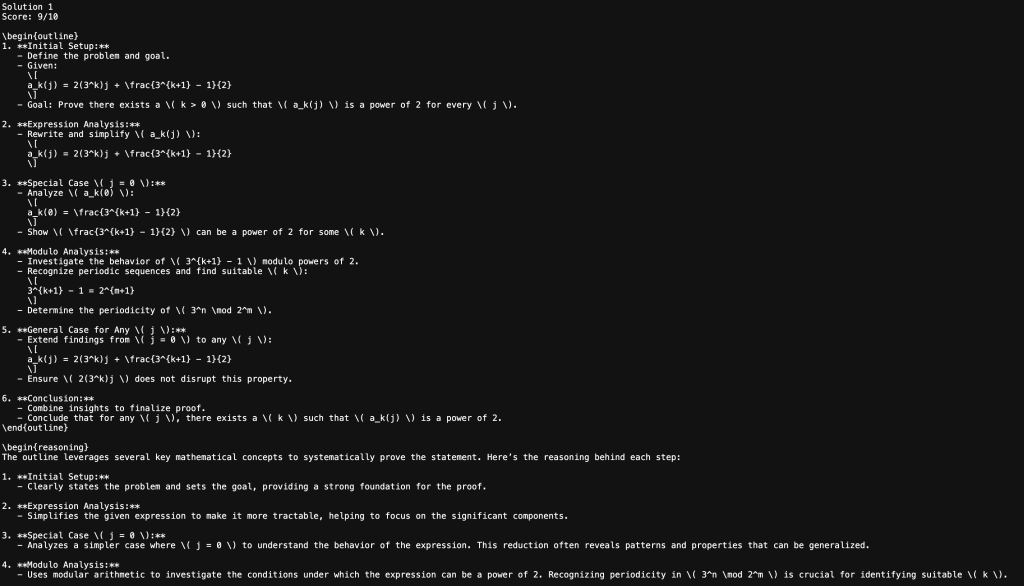
Score: [Your score here]

\\begin{{outline}}
[Your outline here]
\\end{{outline}}

\\begin{{reasoning}}
[Your reasoning here]
\\end{{reasoning}}
"""
    messages.append(HumanMessage(content=user_prompt))

    # Get response from LLM using 'invoke'
    response = llm.invoke(messages).content  # Updated method call
    return response.strip()

def main():
    # Get the math problem from the user
    # math_problem = "Find a function that is bijective, continuous, and whoes floor is exactly equal to the prime number counting function. The function should not make use of prime numbers or of the prime number counting function. Ideally this function should be closed form, however it does not have to be."
    math_problem = "Prove Collatz conjecture"
    
    # For each of the three solutions
    for solution_number in range(1, 4):
        print(f"\nGenerating solution {solution_number}...\n")
        # Reset conversation history
        conversation_history = []

        # Interaction loop
        for iteration in range(1, 11):  # Up to 10 iterations
            print(f"Iteration {iteration}")
            # Each agent reads the conversation history and produces a response
            for branch in branches:
                response = agent_response(branch, conversation_history, math_problem)
                conversation_history.append({'agent': branch, 'message': response})
                print(f"{branch}: {response}\n")
            # Moderator reads the conversation and decides whether to terminate
            moderator_decision = moderator_response(conversation_history, math_problem)
            conversation_history.append({'agent': 'Moderator', 'message': moderator_decision})
            print(f"Moderator: {moderator_decision}\n")
            if 'terminate' in moderator_decision.lower():
                break

        # After interactions, get the final outputs from the moderator
        final_output = moderator_final_output(conversation_history, math_problem)
        print(f"Moderator Final Output:\n{final_output}\n")

        # Output the conversation transcript to a text file
        transcript_filename = f"transcript_solution_{solution_number}.txt"
        with open(transcript_filename, 'w') as f:
            for message in conversation_history:
                f.write(f"{message['agent']}: {message['message']}\n\n")

        # Output the outline, reasoning, and score to a text file
        output_filename = f"solution_{solution_number}.txt"
        with open(output_filename, 'w') as f:
            f.write(f"Solution {solution_number}\n")
            f.write(final_output)

        print(f"Solution {solution_number} generated and saved to {output_filename}\n")

if __name__ == '__main__':
    main()